При открытии сундука вы иногда будете получать новую клюшку, которую вы еще не открыли. Вероятность получить новую клюшку зависит от того, сколько карточек находится в сундуке и сколько клюшек вам еще осталось собрать.
Понимание вероятности получения новой клюшки
В каждом сундуке представлены карточки клюшек различного количества и редкости: эпические, редкие или обычные. Для каждой редкости клюшек в сундуке вероятность получения определенных клюшек рассчитывается по следующей формуле:
(Количество карточек клюшек в сундуке ÷ общее количество клюшек этой редкости и тура) × количество еще не открытых в этой редкости и туре клюшек × [0,08].
Если результат равен или больше 100, вы гарантированно получите новую клюшку. Если результат больше 100, вы можете получить несколько клюшек, но не больше трех из одного сундука.
Вероятность получения каждой новой клюшки одинаковая. Все уже имеющиеся в вашей сумке клюшки также обладают одинаковой вероятностью оказаться в наградах.
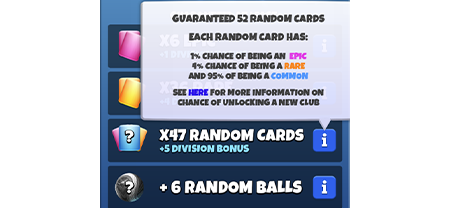
При получении наград сундука будут указаны значения вероятностей эпических, редких и обычных карточек. Например, может быть указано, что каждая обычная карточка обладает вероятностью 1% быть эпической, 4% быть редкой и 95% быть обычной.
При открытии сундука игра определяет редкость каждой карточки в соответствии с указанными значениями вероятности. Затем вышеуказанная формула применяется, чтобы определить, какую карточку вы получите.
Вероятность получения каждой новой клюшки одинаковая. Все уже имеющиеся в вашей сумке клюшки также обладают одинаковой вероятностью оказаться в наградах.
Например:
Предположим, вы открыли сундук, в котором обычных 100 карточек клюшек. На текущем уровне тура в общей сложности представлено 7 обычных клюшек. У вас уже есть 5 из них, так что осталось открыть 2.
- Количество карточек клюшек ÷ общее количество клюшек: 100 ÷ 7 = 14,29
- Умножим на количество еще не открытых клюшек: 14,29 × 2 = 28,57
- Умножим на фиксированный коэффициент (0,08): 28,57 × 0,08 = 2,29
- Умножим на 100, чтобы получить итоговое значение вероятности: 2,29 × 100 = 229
Оно больше 200, поэтому вы гарантированно получите одну новую клюшку (100), останется еще одна полная вероятность гарантированного получения клюшки (следующие 100). Все новые клюшки обладают одинаковой вероятностью получения.
Оставшиеся 29 означают, что с вероятностью 29% вы сможете получить третью клюшку, но так как у вас осталось всего 2 неоткрытых, в этом сундуке вы гарантированно получите только обе эти клюшки.